Física 3ro. Básico : abril 2020

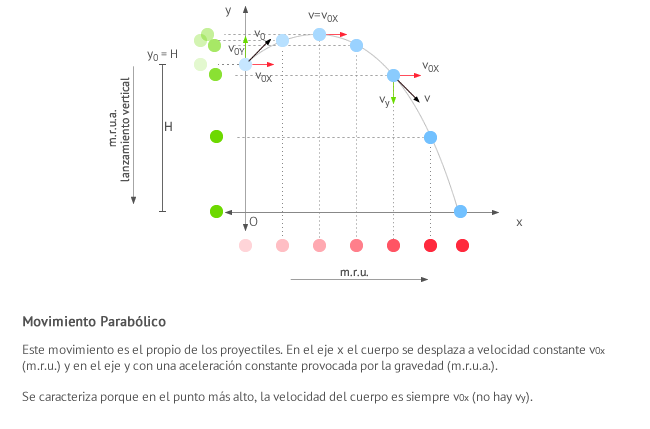
El movimiento parabólico se puede analizar como la unión de dos movimientos. Por un lado, la trayectoria en la proyección del eje de las x (el eje que va paralelo al suelo) describirá un movimiento rectilíneo uniforme. Por otro lado, la trayectoria de la partícula al elevarse o caer verticalmente (en proyección sobre el eje de las y) describirá un movimiento rectilíneo uniformemente acelerado, donde la aceleración es la gravedad

Tipos de movimiento parabólico

Existen diferentes tipos de movimiento parabólico dependiendo desde donde empieza o acaba el movimiento del cuerpo. Por ejemplo:

Movimiento parabólico completo: el cuerpo recorre una parábola completa, empezando y acabando en el suelo.
Movimiento de media parábola: el cuerpo empieza el movimiento desde cierta altura y es lanzado parabólicamente con una fuerza horizontal, en un punto que sería el punto más alto de la parábola completa ideal.
Otros movimientos parabólicos: existen muchos casos particulares del movimiento parabólico, por ejemplo el lanzamiento de una pelota desde el suelo a la terraza de una casa o el lanzamiento a canasta de un jugador de baloncesto. Siempre son tramos de una teórica parábola completa.

Todos los elementos de los movimientos parabólicos se pueden calcular a partir del movimiento parabólico completo.

Dibujo de los tipos de movimiento parabólico

Formulas

1.- Para calcular la altura máxima, aplicamos:

$\displaystyle h=\frac{{{v}_{0}}^{2}se{{n}^{2}}\theta }{2g}$

2.- Para calcular el alcance , aplicamos:

$\displaystyle R=\frac{{{v}_{0}}^{2}sen2\theta }{g}$

3.- Para calcular el tiempo total, aplicamos:

$\displaystyle {{t}_{t}}=\frac{2{{v}_{0}}sen\theta }{g}$

4.- Para calcular la posición de un proyectil en un determinado tiempo

Para x es :

$\displaystyle x={{v}_{0x}}t$

Para y es:

$\displaystyle y={{v}_{0y}}t-\frac{1}{2}g{{t}^{2}}$

5.- Para calcular el tiempo en la altura máxima es:

$\displaystyle t'=\frac{{{v}_{0y}}}{g}$

Ahora es momento de pasar a los ejercicios resueltos del tiro parabólico.

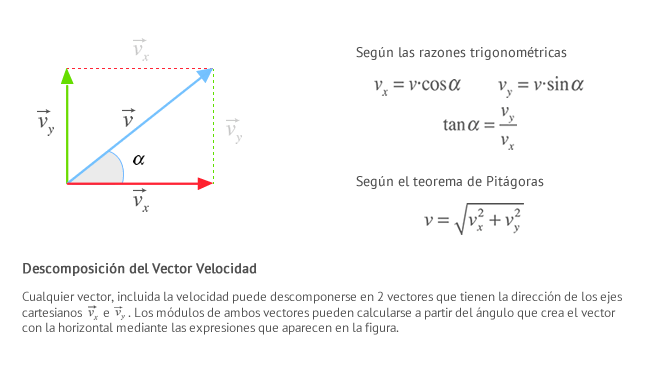
6.- Para descomponer la forma rectangular del vector velocidad es:

$\displaystyle \begin{array}{l}{{v}_{0x}}={{v}_{0}}\cos \theta \\{{v}_{0y}}={{v}_{0}}sen\theta \end{array}$

7.- Para obtener la magnitud de la velocidad en un determinado punto es:

$\displaystyle v=\sqrt{{{\left( {{v}_{0x}} \right)}^{2}}+{{\left( {{v}_{0y}} \right)}^{2}}}$

8.- Para obtener la velocidad en “y” en un determinado tiempo.

$\displaystyle {{v}_{y}}={{v}_{0y}}-gt$

Con esto tenemos para poder resolver nuestros primeros ejemplos.

9.- Para calcular el alcance teniendo el tiempo total y velocidad en “x”.

$\displaystyle x={{v}_{0x}}{{t}_{t}}$

Tarea : Realizar los siguientes ejercicios en su cuaderno e ilustrarlo.

Problema 1.- Un jugador de Fútbol Americano patea el balón con una velocidad de 30 m/s, y éste mismo lleva un ángulo de elevación de 48° respecto a la horizontal. Calcule; a) Altura, b) Alcance, c) Tiempo que permanece en el aire

Problema 2.- Se dispara un proyectil con una velocidad inicial de 80 m/s y un ángulo de 30°, por encima de la horizontal. Calcular: a) Posición y velocidad después de los 6s b) Tiempo para alcanzar la altura máxima c) Alcance horizontal

Problema 3.- Una máquina lanza un proyectil a una velocidad inicial de 110 m/s , con ángulo de 35°, Calcular: a) Posición del proyectil a los 6s, b) Velocidad a los 6s, c) Tiempo en la máxima altura, d) Tiempo total del vuelo, e) Alcance logrado

Problema 4. Un jugador de los Patriotas de la NFL le pega al balón con un ángulo de 37° con respecto al plano horizontal, imprimiéndole una velocidad inicial de 15 m/s, tal como se muestra en la imagen de abajo. Calcule: a) el tiempo que dura la pelota en el aire, b) La altura máxima, c) El alcance horizontal

Problema 5. Una bala se lanza con una velocidad inicial cuya magnitud es de 200 m/s, si se desea que dicha bala golpee a un blanco que está localizado a 2500 metros, entonces calcule: a) El ángulo con el cual debe ser lanzada, b) El tiempo que tarda en llegar al blanco

El movimiento parabólico, también conocido como tiro oblicuo, consiste en lanzar un cuerpo con una velocidad que forma un ángulo α con la horizontal. En la siguiente figura puedes ver una representación de la situación.

El movimiento parabólicoo tiro oblicuo resulta de la composición de un movimiento rectilíneo uniforme (mru horizontal) y un movimiento rectilíneo uniformemente acelerado de lanzamiento hacia arriba o hacia abajo (mrua vertical).

Ecuaciones

Las ecuaciones del movimiento parabólico son:

Las ecuaciones del m.r.u. para el eje x

$x = x 0 + v x \cdot t$
Las ecuaciones del m.r.u.a. para el eje y

$v y = v 0 y + a y \cdot t$

$y = y 0 + v 0 y \cdot t + 1 2 \cdot a y \cdot t 2$

Dado que, como dijimos anteriormente, la velocidad forma un ángulo α con la horizontal, las componentes x e y se determinan recurriendo a las relaciones trigonométricas más habituales:

Finalmente, teniendo en cuenta lo anterior, que y0 = H , x0 = 0, y que ay = -g , podemos reescribir las fórmulas tal y como quedan recogidas en la siguiente lista. Estas son las expresiones finales para el cálculo de las magnitudes cinemáticas en el movimiento parabólico o tiro oblicuo:

Posición (m)
- Eje horizontal
  
  $x = v x \cdot t = v 0 \cdot cos (α) \cdot t$
- Eje vertical
  
  $y = H + v 0 y \cdot t - 1 2 \cdot g \cdot t 2 = H + v 0 \cdot sin (α) \cdot t - 1 2 \cdot g \cdot t 2$
Velocidad (m/s)
- Eje horizontal
  
  $v x = v 0 x = v 0 \cdot cos (α)$
- Eje vertical
  
  $v y = v 0 y - g \cdot t = v 0 \cdot sin (α) - g \cdot t$
Aceleración (m/s2)
- Eje horizontal
  
  $a x = 0$
- Eje vertical
  
  $a y = - g$

Experimenta y Aprende

-10

-20

t (s) = 0.00

v0 (m/s) = 9.00

α (rad) = 1.24

v0x

v0y

Datos
g = 9.8 m/s2 | H = 30.00 m | α = 1.24 rad

v0 = 9.00 m/s
v0x = v0 · cos(α) = 9.00 · cos(1.24) = 2.92 m/s
v0y = v0 · sin(α) = 9.00 · sin(1.24) = 8.51 m/s

x = vx · t = 2.92 · 0.00 = 0.00 m
y = H + v0y·t - 1/2 · g · t2 = 30.00 + 8.51 . 0.00 - 1/2 · 9.8 · 0.002 = 30.00 m

vx = v0x = 2.92 m/s
vy = v0y - g · t = 8.51-9.8 · 0.00 = 8.51 m/s

Movimiento parabólico

La bola azul de la figura representa un cuerpo suspendido sobre el suelo. Puedes arrastrarlo hasta la altura inicial H que desees y seleccionar la velocidad inicial (v0) con la que se lanzará formando un ángulo (α) con la horizontal. La línea gris representa la trayectoria que describirá con los valores que le has proporcionado.

A continuación pulsa el botón Play. Desliza el tiempo y observar como se calcula su posición (x e y) y su velocidad (vx e vy) en cada instante de su descenso hacia el suelo.

Comprueba como la proyección del cuerpo en el eje y (verde) describe un movimiento de lanzamiento vertical y en el eje x (rojo) describe un movimiento rectilíneo uniforme.

Ecuación de posición y de trayectoria en el movimiento parabólico

La ecuación de posición de un cuerpo nos sirve para saber en qué punto se encuentra en cada instante de tiempo. En el caso de un cuerpo que se desplaza en dos dimensiones, recuerda que, de forma genérica, viene descrita por:

r \to (t) = x (t) i \to + y (t) j \to

Sustituyendo la expresiones anteriores de la posición en el eje horizontal ( m.r.u. ) y en el eje vertical ( m.r.u.a. ) en la ecuación de posición genérica, podemos llegar a la expresión de la ecuación de posición para el movimiento parabólico.

La ecuación de posición del movimiento parabólico viene dada por:

r \to = (x 0 + v 0 x \cdot t) \cdot i \to + (H + v 0 y \cdot t - 1 2 \cdot g \cdot t 2) \cdot j \to

Por otro lado, para saber qué trayectoria sigue el cuerpo, es decir, su ecuación de trayectoria, podemos combinar las ecuaciones anteriores para eliminar t, quedando:

y = H + v 0 y \cdot (x v 0 x) - 1 2 \cdot g \cdot (x v 0 x) 2 = H + k 1 \cdot x - k 2 \cdot x 2 k 1 = v 0 y v x; k 2 = 1 2 \cdot v 0 x 2 \cdot g

Como cabía esperar, se trata de la ecuación de una parábola.

Por otro lado, será frecuente que en los ejercicios te pidan alguno de los siguientes valores.

Altura máxima

Este valor se alcanza cuando la velocidad en el eje y, vy , vale 0. A partir de la ecuación de velocidad en el eje vertical, e imponiendo vy = 0, obtenemos el tiempo t que tarda el cuerpo en llegar a dicha altura. A partir de ese tiempo, y de las ecuaciones de posición, se puede calcular la distancia al origen en el eje x y en el eje y.

Tiempo de vuelo

Se calcula igualando a 0 la componente vertical de la posición. Es decir, el tiempo de vuelo es aquel para el cual la altura es 0 (se llega al suelo).

Alcance

Se trata de la distancia máxima en horizontal desde el punto de inicio del movimiento al punto en el que el cuerpo impacta el suelo. Una vez obtenido el tiempo de vuelo, simplemente sustituye en la ecuación de la componente horizontal de la posición.

Ángulo de la trayectoria

El ángulo de la trayectoria en un determinado punto coincide con el ángulo que el vector velocidad forma con la horizontal en ese punto. Para su cálculo obtenemos las componentes vx y vy y gracias a la definición trigonométrica de tangente de un ángulo, calculamos α:

tan (α) = c a t e t o o p u e s t o c a t e t o c o n t i g u o = v y v x \Rightarrow α = tan - 1 (v y v x)

Ejemplo

Minuto 90 de juego... Lopera se acerca al balón para lanzar un libre directo a 40 metros exactos de la portería, da dos pasos hacia atrássss y lanzaaaa. El balón describe una trayectoria parabólica y sale con una elevación de 20º... y ¡¡¡¡¡GOOOOLLL!!!! ¡¡¡¡GOOOOOOOLLL!!!! ¡¡¡¡El balón entra por la escuadra a 1.70 metros de altura!!!. Tras oir esta emisión en la radio, ¿sabrías responder a las siguientes preguntas?

a) Desde que Lopera chuta y marca el gol, ¿cuánto tiempo ha transcurrido y a qué velocidad salió el balón desde las botas de Lopera?
b) ¿Qué altura máxima alcanzó el balón?
c) ¿Con qué velocidad llegó el balón a la portería?

Solución

Cuestión a)

El instante en el que el balón llega a la portería x=40 m e y=1.7 m. Sustituyendo en las ecuaciones de la posición del movimiento parabólico:

x = v 0 \cdot cos (α) \cdot t y = v 0 \cdot sin (α) \cdot t - 1 2 \cdot g \cdot t 2} \Rightarrow 40 = v 0 \cdot cos (20) \cdot t 1.7 = v 0 \cdot sin (20) \cdot t - 1 2 \cdot 9.8 \cdot t 2} \Rightarrow 40 = v 0 \cdot 0.94 \cdot t 1.7 = v 0 \cdot 0.34 \cdot t - 4.9 \cdot t 2} \Rightarrow t = 1.61 s v 0 = 26.36 m s /}

Cuestión b)

Cuando la componente y de la velocidad (vy) sea 0 entonces quiere decir que estaremos en el punto más alto de la parábola. Recuerda que comienza a ascender y su velocidad en el eje y va disminuyendo hasta que se anula y comienza a ser negativa para descender.

v y = v 0 y - g \cdot t \Rightarrow v y = v 0 \cdot sin (α) - g \cdot t \Rightarrow 0 = 26.36 m s / \cdot sin (20 º) - 9.8 m s 2 / \cdot t \Rightarrow t = 9 . 05 m s / 9 . 8 m s 2 / \Rightarrow t = 0.92 s

Ahora ya estamos en condiciones, aplicando la ecuación de posición en el eje y, y sustituyendo por el instante que hemos obtenido, de determinar la altura máxima alcanzada:

y = H + v 0 y \cdot t - 1 2 g \cdot t 2 \Rightarrow y = 0 + 26.36 \cdot sin (20) \cdot (0.92) - 1 2 \cdot 9.8 \cdot (0.92) 2 \Rightarrow \Rightarrow y = 4.14 m

Cuestión c)

Sabiendo que el balón llegó a la portería en 1.61 s, su velocidad se obtiene:

v x = 26.36 \cdot cos (20) = 24.77 m s / v y = 26.36 \cdot sin (20) - 9.8 \cdot 1.61 = - 6.76 m s / v = v x 2 + v y 2 - - - - - - - - \sqrt = (24.77) 2 + (- 6.76) 2 - - - - - - - - - - - - - - - - \sqrt = 25.67 m s /

Fórmulas

v y = v 0 y - g \cdot t = v 0 \cdot sin (α) - g \cdot t

x = v x \cdot t = v 0 \cdot cos (α) \cdot t

a x = 0

y = H + v 0 y \cdot t - 1 2 \cdot g \cdot t 2 = H + v 0 \cdot sin (α) \cdot t - 1 2 \cdot g \cdot t 2

a y = - g

v x = v 0 x = v 0 \cdot cos (α)

Actividad: Realizar formulario de los temas visto, tomar nota en el cuaderno de los ejemplos de los videos, tomarle foto y enviármela.

Física 3ro. Básico

miércoles, 22 de abril de 2020

Movimiento Parabólico